Sort

排序

堆排序

堆构建过程

什么是堆？

​ 堆就是用数组实现的二叉树，所以它没有使用父指针或者子指针。堆根据“堆属性”来排序，“堆属性”决定了树中节点的位置

定义

通常堆是通过一维数组来实现的。在数组起始位置为0的情形中：

• 父节点i的左子节点在位置：2i+1
• 父节点i的右子节点在位置：2i+2
• 子节点i的父节点在位置：i/2 -1
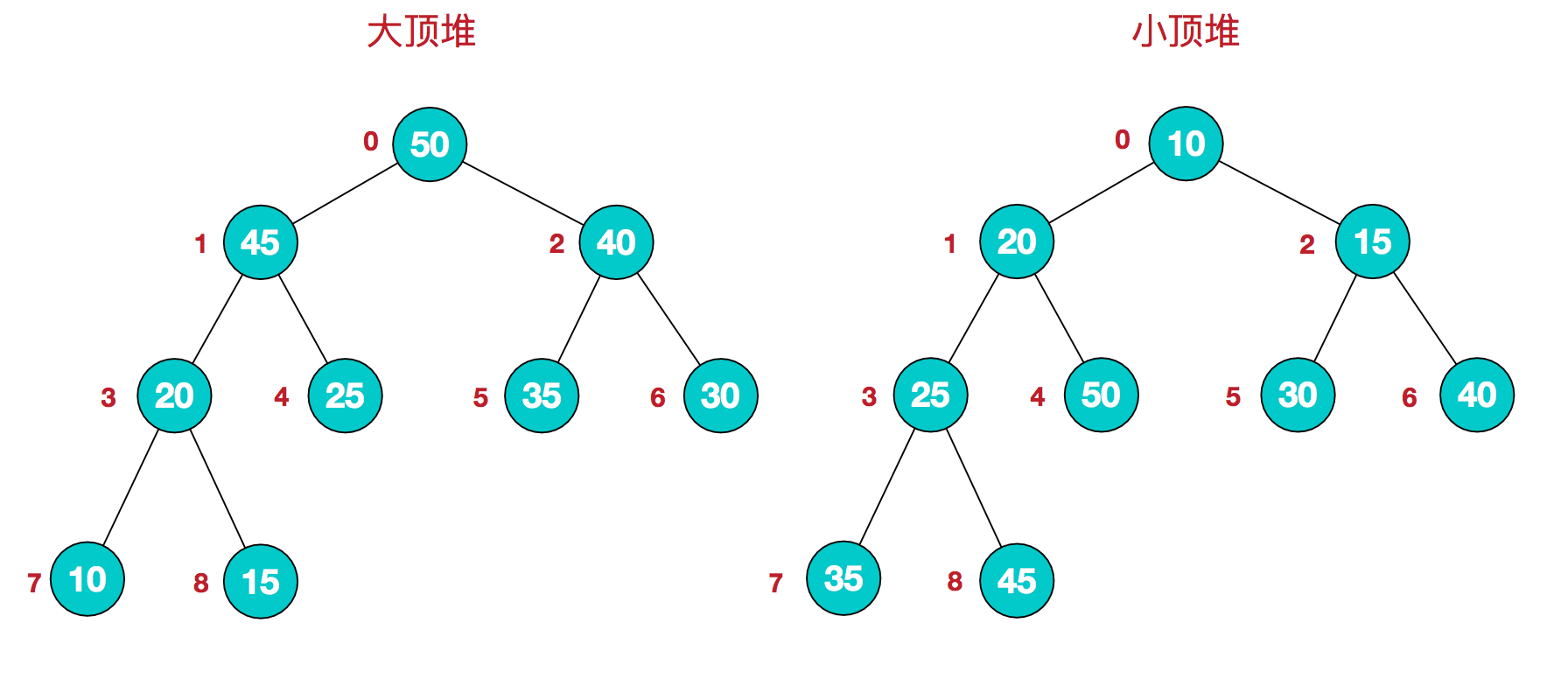
• 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列
• 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列

堆的操作

在堆的数据结构中，堆中的最大值总是位于根节点（在优先队列中使用堆的话堆中的最小值位于根节点）。堆中定义以下几种操作：

• 最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
• 创建最大堆（Build Max Heap）：将堆中的所有数据重新排序
• 堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

JUC中的优先级队列就是使用小顶堆来实现的

堆排序算法步骤

1. 将待排序的数组初始化为大顶堆，该过程即建堆

2. 将堆顶元素与最后一个元素进行交换，除去最后一个元素外可以组建为一个新的大顶堆

3. 由于第二步堆顶元素跟最后一个元素交换后，新建立的堆不是大顶堆，需要重新建立大顶堆。重复上面的处理流程，直到堆中仅剩下一个元素

代码实现

public class HeapSort {
    private int[] arr;

    public HeapSort(int[] arr) {
        this.arr = arr;
    }

    public void sort() {
        int len = arr.length - 1;
        // 获取最后一个子节点
        int beginIndex = (len >> 1) - 1;

        // 构建一个大顶堆
        for (int i = beginIndex; i >= 0; i--) {
            maxHeap(i, len);
        }

        // 将堆顶元素和队尾交换
        for (int i = len; i > 0; i--) {
            // 将堆顶元素和最后一个元素交换
            swap(0, i);
            // 将最大值给到堆尾后，破坏了最大堆，除去最后一个元素外继续构建大顶堆
            maxHeap(0, i - 1);
        }
    }

    /**
     * 构建大顶堆
     *
     * @param index
     */
    public void maxHeap(int index, int len) {

        // 求左子节点
        int left = (index << 1) + 1;
        // 求右子节点
        int right = left + 1;
        // 当前堆的最大值，默认左子节点 (下标)
        int max = left;

        // 左节点越界，直接结束
        if (left > len) {
            return;
        }

        // 判断计算出来的右子节点是否越界, 获取子节点最大的
        if (right <= len && arr[right] > arr[left]) {
            max = right;
        }

        // 子节点和当前堆顶比较，对调堆顶
        if (arr[max] > arr[index]) {
            swap(max, index);
            maxHeap(max, len);
        }
    }

    public void compare(int num) {
        // 判断小顶堆堆顶是否小于当前值，是则替换
        if (arr[0] < num) {
            arr[0] = num;
            // 重建小顶堆
            sort();
        }
    }


    /**
     * 构建小顶堆
     *
     * @param index
     * @param len
     */
//    public void minHeap(int index, int len) {
//
//        // 求左子节点
//        int left = (index << 1) + 1;
//        // 求右子节点
//        int right = left + 1;
//        // 当前堆的最大值，默认左子节点 (下标)
//        int min = left;
//
//        // 左节点越界，直接结束
//        if (left > len) {
//            return;
//        }
//
//        // 判断计算出来的右子节点是否越界, 获取子节点最大的
//        if (right <= len && arr[right] < arr[left]) {
//            min = right;
//        }
//
//        // 子节点和当前堆顶比较，对调堆顶
//        if (arr[min] < arr[index]) {
//            swap(min, index);
//            minHeap(min, len);
//        }
//    }
    public void swap(int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }


    /**
     * 测试用例
     * <p>
     * 输出：
     * [0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9]
     */
    public static void main(String[] args) {
        int[] arr = new int[]{3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6};
        new HeapSort(arr).sort();
        System.out.println(arr);
    }
}

经典 Top K 问题

除了排序外，经常还利用大顶堆、小顶堆解决 Top K 问题

大顶堆： 从N个数中找出最小的K个

小顶堆：从N个数中找出最大的K个

核心思想：最大K个，先获取K个值，建立小顶堆。然后遍历 K～N的元素，与堆顶比较，元素比堆顶大则进行替换。然后再重新构建小顶堆。当循环多次后，堆顶能够过滤掉大部分数据

Top K 也能使用一个长度为K的链表进行排序，记录最大值和最小值（链头，链尾），然后循环K～N的元素进行比较，如果元素最小值<元素则从链表头部插入，如果元素>最大值则从链表尾部插入，值相等不插入，当链表超过K长度，修剪链表头部 (海量数据TOP K 数据漏斗思想)

实现

/**
 * @description:
 * @author: ken 😃
 * @create: 2022-03-11 10:26
 * 从一亿的数组中获取最大的K个
 **/
public class Heap {
    public static Random RANDOM = new Random();
    public static int[]  arr    = new int[1000];

    // 堆初始化
    public static void init() {
        int len         = arr.length - 1;
        int lastSubNode = (len >> 1) - 1;

        for (int i = lastSubNode; i >= 0; i--) {
            minHeapIfy(i, len);
        }
    }

    // 构建小顶堆算法
    public static void minHeapIfy(int currentIndex, int len) {
        int left       = (currentIndex << 1) + 1;
        int right      = left + 1;
        int subNodeMin = left;

        if (left > len) {
            return;
        }

        if (right <= len && arr[right] < arr[left]) {
            subNodeMin = right;
        }

        if (arr[subNodeMin] < arr[currentIndex]) {
            // 堆顶置换
            swap(subNodeMin, currentIndex);
            // 递归让置换的直接点继续保持最小堆特性
            minHeapIfy(subNodeMin, len);
        }
    }

    // 元素和堆顶比较
    public static void compare(int num) {
        if (arr[0] < num) {
            arr[0] = num;
            // 保持小顶堆
            init();
        }
    }

    public static void swap(int i, int k) {
        int temp = arr[i];
        arr[i] = arr[k];
        arr[k] = temp;
    }

    public static int getNum(int min, int max) {
        return RANDOM.nextInt(max - min + 1) + min;
    }

    public static void main(String[] args) {

        // 数据初始化
        int[] data = new int[100000000];
        for (int i = 0; i < data.length; i++) {
            data[i] = getNum(0, 100000);
        }

        // 随机设置个最大值，测试是否正确
        data[getNum(0, 50000000)] = 999999999;

        // 获取前K个组成小顶堆
        long start = System.currentTimeMillis();
        arr = Arrays.copyOfRange(data, 0, 1000);

        for (int i = 1000; i < data.length; i++) {
            compare(data[i]);
        }

        Arrays.stream(arr).forEach(System.out::println);
        System.out.println(String.format("耗时: %s", (System.currentTimeMillis() - start) / 1000.f));
    }
}